Surviving the harsh lunar
environment is apparently one of mankind's greatest engineering achievements.
The space suit worn by the Apollo astronauts on the surface of the moon had to protect them from UV, X, and gamma-rays, heat, and solar flare radiation from the sun; cosmic rays; micro meteors; regulate humidity, carbon dioxide and oxygen; and maintain a pressurised layer of air.
The space suit worn by the Apollo astronauts on the surface of the moon had to protect them from UV, X, and gamma-rays, heat, and solar flare radiation from the sun; cosmic rays; micro meteors; regulate humidity, carbon dioxide and oxygen; and maintain a pressurised layer of air.
Amazing life-saving suit technology: the state of the art in 1969. The Apollo 11 suit.
Without an atmosphere to keep
them cool, the astronauts could get as hot as 107C in the sunlight on the
surface of the moon. The astronauts were
kept cool by a liquid cooling garment worn under the space suit.
Remarkably, there's no record of a test of one of these suits, with their cooling system, working on an astronaut in full vacuum conditions on earth before their use in space.
Remarkably, there's no record of a test of one of these suits, with their cooling system, working on an astronaut in full vacuum conditions on earth before their use in space.
The astronauts in training on
earth were in full earth atmospheric pressure, using umbilical tethers connected to
standard air conditioners.
Not having an atmosphere to
exchange heat with, air conditioners of the regular type would not work on the
moon. To overcome this problem NASA
commissioned Hamilton Standard (HS) to supply them with the
porous plate sublimator.
I've been told by a reliable
source (a blogger on the internet actually) that the porous plate sublimator is
a standard technology used extensively by the Americans, Russians and other
countries in space, and is practically available off the shelf. Really?
Well, my investigations painted a somewhat different picture.
For example, there is no
Wikipedia page on the porous plate sublimator.
There are no technical details to be found in any engineering reference
on it, only the most general of descriptions.
There are no data sheets, pictures, charts,
graphs, or specifications to be found on the internet. NASA
has never demonstrated one working in a vacuum chamber here on earth. And you certainly can't buy one, not even
second hand.
The only information available on
the internet I could find were a few old patents and two documents concerning
the actual working of it. The first document is a final report by Hamilton Standard
published in 1965[1]. The second is a thesis for a PhD received in 1970 by James Shero of Rice University[2].
***************************************
A sintered nickel porous plate
consists of small balls of nickel that are brought up to a temperature just
below the melting point. By staying
below the melting point, the balls fuse together while not melting, thus
retaining the gaps in between.
Bronze sintered metal plate
Nickel sintered metal plate. The 2 - 4 micrometre particle size demonstrated in the plate above is similar to the pore size in plates used by HS and Shero.
HS and Shero mention several possible modes of operation:
A) Sublimation
B) Glacial
C) Boiling
D) Mixed (a combination of
sublimation and boiling)
*******************************
A) Sublimation mode
In sublimation mode water freezes
in the pores of the plate and heat is removed from the system by sublimation to
the vacuum of space.
Ice will generate some heat as it
freezes from liquid to solid form due to the heat of fusion. Water has an unusually high latent heat of
evaporation/sublimation which can more than compensate for the heat generated
upon fusion (freezing), as well as any heat that might be generated by friction
as the water moves through the plate.
In order for the water to get
cold enough to freeze, it must first lose heat by the water boiling from a
liquid, rather than a solid, state (see boiling mode below).
Some suggest that boiling isn't
necessary to produce ice at the outer pores of the plate -- ice will
freeze because space is cold. In fact,
unlike earth which has an atmosphere with some heat capacity, space doesn't
have a temperature and is neither hot nor cold (more here).
HS and Shero both mention that
without freezing, breakthrough of the water to the vacuum was an ever-present
problem. Ice in pores is useful for blocking water flow, but the expansion of the ice would shatter the plate.
HS found the unreinforced sintered plates to be brittle. They could fracture easily (pg 20 - 21 [1]). HS also found that brazed versions of the porous plates weren't much stronger.
The expansion of ice in the pores has the effect of ripping the plate apart. HS said such a fracture would result in a thin sliver of ice emanating from the porous plate. In reality such a rupture would let liquid water leak to space, ruining the cooling effect of the sublimator.
In order to continue their experiments, HS
used another unspecified bonding technique for the spheres composing the porous
plate. It's odd for them not to test the
material that was supposed to be used in the final product, especially as this
was HS's final report.
B) Glacial mode
The above scenario of ice
freezing in the pores of the plate has been suggested by some, but is not how HS
and Shero actually portray the sublimation mode.
HS and Shero claim another type of sublimation mode exists, which
I have dubbed the glacial mode, because Shero describes the ice sheet as
advancing like a glacier (pg 5 of [2]).
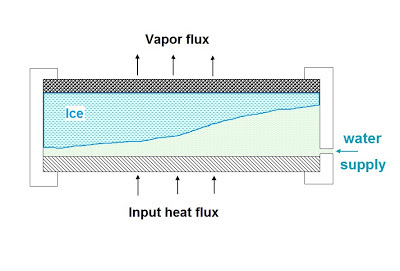
In glacial mode a layer of ice
forms behind the plate, rather than inside it.
This ice sheet was claimed to
have been observed by HS and Shero in their lab tests. By having such a layer of ice inside the
surface of the plate, the mode solves a couple of problems: 1) Because the ice is behind rather than in the
pores of the plate, cracking due to the expansion of ice within the pores is avoided. 2) The ice layer also stops breakthrough of the
water to the vacuum by forming a seal that the water cannot get past.
But the layer of ice introduces
other problems. With no ice or liquid in
the plate, just water vapour, it's not clear how the porous plate now sustains
a pressure drop across it. Even with
steam going through the plate, with steam's low viscosity, the outside face of
the ice sheet, just inside the plate, will be near 0 psi, just like the vacuum is on the
outside of the plate.
This means that from the inside
to the outside of the ice sheet there is difference of about 5 psi (33kPa or
1/3 atmosphere). That's a lot of
pressure for the ice sheet to sustain.
It would be unlikely for the ice sheet to move forward in a uniform manner; for it not to crack and let water slip past; and for it to retain a constant thickness.
It would be unlikely for the ice sheet to move forward in a uniform manner; for it not to crack and let water slip past; and for it to retain a constant thickness.
And imagine how easy would it be for
the whole chamber to freeze solid, thus altering the conduction properties of
it, and changing the whole heat rejection capability of the sublimator. All of these uncertainties would endanger the life of the astronaut.
Both HS and Shero depict the water
feedpipe as being on one side of the liquid chamber. That would make the side of the chamber, with
fresh feedwater coming in, have a much thinner ice sheet:
Surely an uneven ice sheet would be created: thinner where the water comes in where there would be turbulent flow, and thicker in the far corner where the water stagnates. This would affect the performance of the sublimator. Yet, such an effect was never mentioned by HS or Shero.
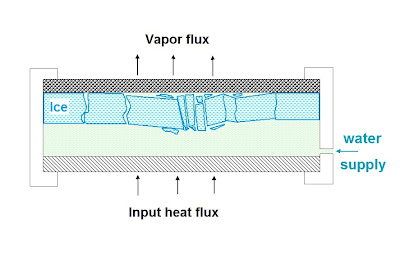
Another problem with the scenario
is that the ice would expand by 10% and press against the sides of the
sublimator walls. This expansion would
press against the walls of the chamber possibly damaging it, like water pipes
bursting in the winter; and the increased friction with the walls would stop it
from moving forward, especially at the edges.
The expansion could also make the ice crack and buckle
especially toward the middle of the sheet.
Glacial mode: Not all it's cracked up to be. Ice would expand, crack and damage the equipment, and let water leak out to space.
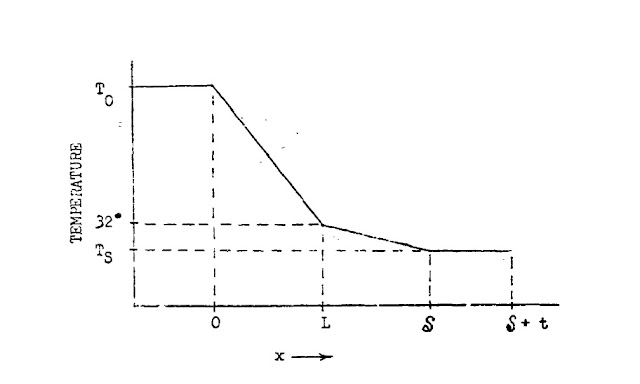
Below is HS's diagram (pg 52 [1]) of the
heat flow across the system depicted above (Fig "HS" above). The gradient of temperature drop across the
water is roughly 5.5 times that through the ice.
This would be okay if both
substances were solid and ice had roughly 5.5 times the thermal conductivity of
water. As it happens, ice's thermal
conductivity is about 4 times that of water. But that's only in terms of conduction -- as
though water had no ability for convection.
By the time convection is
factored in, water could be many times a better conveyor of heat than ice
(depending on the size of the volume water can convect in).
In the graph above, considering
the steep gradient of the line from 0 to L, with convection factored in, heat
is arriving at a much faster rate at L than it is being removed across the ice layer
from L to S. This will have the effect
of building up heat at the ice-liquid interface L, gradually melting it and
reducing the ice layer until it's all gone; thus maximizing heat transfer
across the gap.
This is therefore clearly not a mode that
is sustainable or realistic. The only
real way to maintain an ice layer in such a fashion would be to insert
refrigeration coils into it, in order to extract enough heat. (Obviously that would be cheating -- you can't have such refrigeration coils on the moon).
C) Boiling mode
Like most metals, nickel is
hydrophilic, meaning easily wet by water.
Therefore, water will be readily drawn into the pores of the plate, such
that when the water is static, the porous plate provides no barrier to the
water, and will not constrain it from escaping to the vacuum of space.
HS and Shero contradict this
claim. HS makes the following statement
on page 11 [1]:
The absence of a solid ice layer to prevent liquid from passing through the porous plate requires that some other mechanism retain the liquid....It was found that surface tension supplies the necessary restraining force...The head of liquid which a pore can retain by surface tension is inversely proportional to the equivalent size of the restriction. Thus, in sintered metal powder plates, liquid enters the pores until the integrated restrictive force balances the pressure differential.
Even if surface tension were to increase with decreased pore size, the number of pores goes up in
equal measure. The greater number of pores counters the alleged inverse proportionality
of the "restrictive" force.
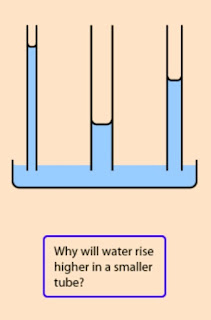
Anyway, the claim is nonsense because, while the capillary force does decrease as the radius of the pore, the surface tension increases as the square of decrease in pore size. In combination with capillary force, the surface tension has the effect of drawing the liquid into the plate, like water moves up in these straws:
Anyway, the claim is nonsense because, while the capillary force does decrease as the radius of the pore, the surface tension increases as the square of decrease in pore size. In combination with capillary force, the surface tension has the effect of drawing the liquid into the plate, like water moves up in these straws:
On page 20 HS admits it didn't
test the effect of plate wettability on water retention stating:
These hypotheses were not examined experimentally.
They could apparently afford to
be confident in this regard because the pressure of the steam generated by the
boiling was supposed to restrain the water, no matter the plate's wettability. It's true, steam expansion does create
pressure, but only if it is constrained.
Being unbounded on one side, the steam will escape to space, providing little barrier to the water from creeping forward.
Being unbounded on one side, the steam will escape to space, providing little barrier to the water from creeping forward.
The steam would have to create a considerable dynamic force if it was to have any back pressure to stop the water. But steam has 50 times less viscosity than water, so it's hard to see how this vapour can have enough back force to prevent water breakthrough.
And if the steam really were to
stop the flow of water, such a drop in water flow would immediately eliminate the dynamic
pressure drop in the water, such that the water would creep forward again until
it escaped to space.
Even if the nickel
plate were hydrophobic (water rejecting) instead of hydrophilic, the
breakthrough would be an all or nothing proposition. Once the pressure pushed the water through
the inside face of the plate it would go all the way through to the outside
face.
Whatever the case may be, any static
force, such as surface tension, or capillary force etc, is not one that can
create a pressure drop, like a gradient, across the
plate (see diagram below).
A dynamically created pressure
drop could do this by resisting flow in one direction. As water moves through the plate, it collides
with the walls of the pores, and loses kinetic energy and pressure.
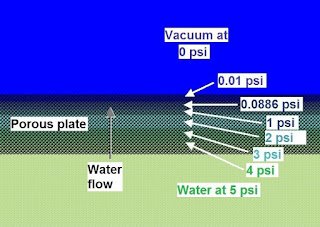
Example of how pressure drop should look across the porous plate
For water to boil at room
temperature the pressure must reduce to 0.0886 psi.
This pressure must be reached inside the plate or the water will not
boil inside it, water will escape to space unboiled, and heat will not be
extracted from the system.
The problem with this method of dynamic
pressure drop is that the amount of water flow necessary to create a 5 to 0 psi
pressure drop is so large that the system would be drained of its 5.2 litres of
water in a matter of seconds, not the hours that were required to sustain the
astronauts during their lunar EVAs.
Using data from the Shero document, for example, the following calculations can be made using an online pressure drop calculator:
Using data from the Shero document, for example, the following calculations can be made using an online pressure drop calculator:
Typical results using pressure drop calculator of water flowing through a perforated orifice plate. You need many litres per second to get a 5 psi pressure drop. (Parameters from Shero plates 2 and 10, Table 1 pg 58 of [2])
Another consideration is that,
the pressure drop wouldn't be linear across the plate.
Because the pressure drop is proportional to the flow of water, the flow and the resistive force, would be greater at the entrance of the plate and less at the exit. And as the pressure tends to zero, so does the velocity of the fluid through the plate -- a self-neutralising effect.
Because the pressure drop is proportional to the flow of water, the flow and the resistive force, would be greater at the entrance of the plate and less at the exit. And as the pressure tends to zero, so does the velocity of the fluid through the plate -- a self-neutralising effect.
From all of the above it can be
seen that the porous plate is not a device that can create the necessary pressure
drop from 5 psi on the inside of the plate to 0 psi on the outside.
The porous plate is therefore an open valve to space. All the water would leak out in a matter of seconds or minutes and the cooling system would fail.
The porous plate is therefore an open valve to space. All the water would leak out in a matter of seconds or minutes and the cooling system would fail.
D) Mixed mode
Given the different pore sizes in
the plate, different pores would be at different pressures or temperatures, resulting
in ice in some areas and water in others. This was called mixed mode by HS and Shero.
Given the high conductivity of heat through the nickel of the plate (compared to water and ice), it's hard to see how different parts of it can be at significantly different temperatures.
Given the high conductivity of heat through the nickel of the plate (compared to water and ice), it's hard to see how different parts of it can be at significantly different temperatures.
Furthermore, if different parts
of the plate have differing phases of water, heat flow through the
plate would be different in different places. This could affect the porous plate's heat
rejection operation, yet such considerations were never raised by HS or Shero.
It's basically a bet each way: HS and Shero claim that if it doesn't work in the sublimation mode it works in the evaporation mode and vice versa. It's like: it works one way or the other, and it'll all be OK on the day, trust us.
It's basically a bet each way: HS and Shero claim that if it doesn't work in the sublimation mode it works in the evaporation mode and vice versa. It's like: it works one way or the other, and it'll all be OK on the day, trust us.
If it really were true that the
machine operated in evaporative mode, sublimation mode or a combination of the two,
consider that although the small pore sizes restrict convection, there would
still be quite a difference in rate of mass loss between a pore that was boiling and a
pore that was sublimating. Imagine how different the heat rejection rates would be in modes a), b) or c) above.
Yet this difference was not considered by HS or Shero.
Yet this difference was not considered by HS or Shero.
In a boiling volume of water steam comes
from any place within the material; and the action of convection supercharges
the release. By contrast, sublimation is
a much slower process, occurring only on the surface, and is more akin to
the process of evaporation in water, than boiling.
The different rate would make the sublimator behave in very different ways depending on if it was in sublimation mode or boiling mode, making the sublimator unreliable as a rejector of heat.
The different rate would make the sublimator behave in very different ways depending on if it was in sublimation mode or boiling mode, making the sublimator unreliable as a rejector of heat.
*********************************
As well as the above considerations consider what would happen every time an
astronaut jumped up and down to do a jump salute; fell down; or swung around rapidly. And consider all of those bumps that would be
endured when the astronauts were driving in their lunar buggy.
All these movements would put huge forces and strains on the plate, and would greatly vary the pressure through it. This could cause the operation of the plate to change, or for the water to leak out.
All these movements would put huge forces and strains on the plate, and would greatly vary the pressure through it. This could cause the operation of the plate to change, or for the water to leak out.
Finally, it was noticed by HS
that the nickel plates would oxidise with time; and that the water would
become contaminated with time. Both
these things would affect the plate's wettability and change the sublimator's
heat rejection capability.
That seems like a dangerous aspect of the device to leave untested,
especially at the time of HS's final report in 1965.
Conclusion:
One could argue that all these problems were worked out later than HS's report, yet there's is no
indication that was the case in any of the literature. Shero was still investigating fundamental
aspects, such as plate wettability, when the moon landings were supposedly already
underway in July of 1969.
Other than Hamilton Standard, the
only apparently independent testing of the device was by Shero of Rice
University; and yet Rice University, and Shero's project, was a recipient of
funding from NASA, so it wasn't really that independent.
NASA is, after all, just another
branch of the government, like the Department of Defense, and would have been
used any way the American government saw fit in its cold war effort against the Soviet
Union.
HS and Shero fulfilled their role as best they could: to provide a plausible theoretical basis for something that might work...maybe. HS also provided some hardware. Beyond that NASA was solely responsible for the final assembly and use of the device.
Whether or not it ultimately worked at the time of the moon landing only NASA knows.
HS and Shero fulfilled their role as best they could: to provide a plausible theoretical basis for something that might work...maybe. HS also provided some hardware. Beyond that NASA was solely responsible for the final assembly and use of the device.
Whether or not it ultimately worked at the time of the moon landing only NASA knows.
References:
[1] Hamilton Standard
(HS), Sangiovanni and Hepner. Porous
Plate Water Boiler Design Study, Final Report, May 20, 1965. Hamilton
Standard Report: HSER 3509. (Link)











In your posting, you have done a pretty good job exposing the difficulties in attempting to apply sublimation as the working mode for a space-vacuum water cooling system. You have pointed out just about every way in which this principle won't work. So, what exactly was NASA's method of choice? You have dug up a couple reports - from 1965 and 1969 - that attempt to describe a method for cooling a suit - the porous nickel plate sublimator - but is this actually what NASA ended up using? Utilizing a sintered nickel plate seems to be wrought with too many obstacles. Over the past several years, closely studying diagrams and photos of the suits, I have not seen any evidence of such a device being employed. The backpack appears to be tightly filled with various apparatus and breathing supplies, but no consideration for thermal management.
ReplyDeleteWouldn't a simpler approach avoiding ice (and sublimation) be just a good? Perhaps a metered flow of water through an orifice, surrounded by a constant flow of warm water from the suit? If the orifice were designed in such a way to incorporate a ported manifold conveying warm water from the suit, it would be prevented from freezing while boiling its own supply of feed water into vapor from the extreme vacuum of space. The orifice - or multi-port nozzle - might provide all the cooling effect necessary to maintain the circulating water at a comfortable temperature. Just a thought...